Velocidad de ejecución de la primera repetición en una serie

Velocidad de ejecución de la primera repetición en una serie

En este artículo se expone de manera ordenada la importancia de la velocidad de ejecución de la primera repetición para la dosificación, control y evaluación del entrenamiento de fuerza con el fin de dar la oportunidad de que se pueda tomar conciencia de la repercusión que tiene la adecuada aplicación de esta variable en el jesarrollo de todo lo relacionado con el entrenamiento de fuerza.

En esta serie de artículos tratamos algunos conceptos mas importantes del entrenamiento de fuerza recogiendo notas del reciente libro publicado Fuerza Velocidad y Rendimiento Físico y Deportivo escrito por los reconocidos investigadores Juan José González Badillo y Juan Ribas Serna.

RESUMEN

• El control de la velocidad viene a superar la serie de inconvenientes que presenta la utilización de la RM y de la XRM o nRM en la dosificación del entrenamiento y en la evaluación de su efecto.
• Se ha podido confirmar que cada porcentaje de 1RM tiene su propia velocidad para cada ejercicio. Esta velocidad es muy estable para la misma persona cuando se modifica su rendimiento, y muy semejante entre las personas, incluso cuando el nivel de rendimiento entre personas es muy distinto.
• Si se puede medir la velocidad media o media propulsiva máxima con la que esplaza una masa, al aplicar estas ecuaciones podemos obtener el porcentaje de la RM que resenta dicha masa.
• La velocidad de la primera repetición de la serie sirve para determinar con qué carga relativa se está entrenando el sujeto, asi como para determinar cuál ha sido, y va siendo, el efecto del entrenamiento cada día, cuál ha sido la evolución de la intensidad máxima utilizada cada día, y cuál ha sido el efecto pre-post entrenamiento…
• La velocidad con cada porcentaje es muy semejante entre personas con un nivel de rendimiento muy distinto.

 

Efectivamente, ante todos estos inconvenientes, es necesario encontrar una solución adecuada. Si la programación del entrenamiento no es más que la expresión de una serie o sucesión ordenada de esfuerzos que guardan una relación de dependencia entre sí, y el esfuerzo es el grado real de exigencia en relación con las posibilidades actuales del sujeto, lo cual representa el carácter del esfuerzo, la solución adecuada será conseguir medir con alta precisión el carácter del esfuerzo. Esto se consigue si se conoce:

• El Grado de Esfuerzo que representa la primera repetición de una serie.
• El Grado de Esfuerzo que representa la pérdida de velocidad dentro de la serie.

En este artículo se tratará sobre estos dos factores como elementos clave de la cuantificación, dosificación, control y evaluación de la carga de entrenamiento y de sus efectos.

La velocidad con cada porcentaje de la RM y su estabilidad. Grado de Esfuerzo que representa la primera repetición de una serie

Hace algunos años el profesor González-Badillo escribía: “si pudiéramos medir la velocidad máxima de los movimientos cada día y con información inmediata, este sería posiblemente el mejor punto de referencia para saber si el peso es el adecuado o no”… “también se podría registrar la velocidad máxima alcanzada por cada levantador con cada tanto por ciento, y en función de esto valorar el esfuerzo” (González Badillo, 1991, p. 172), Actualmente se puede afirmar que estas propuestas-hipótesis se han confirmado.

En el año 2000 estos autores presentaron los primeros datos en relación con la velocidad con cada porcentaje (González-Badillo, 2000). Posteriormente se ha podido confirmar que cada porcentaje de 1RM tiene su propia velocidad. Esta velocidad es muy estable para la misma persona cuando se modifica su rendimiento, y muy semejante entre las personas, incluso cuando el nivel de rendimiento entre personas es muy distinto (González-Badillo y Sánchez-Medina, 2010).

Por tanto, en todo el planteamiento sobre la aplicación que tiene el conocimiento de la velocidad de la primera repetición ante una carga absoluta, se parte del supuesto de que, si bien el valor de 1RM puede cambiar entre los distintos días, la velocidad a la que se realiza cada porcentaje de la RM es muy estable.

Por ejemplo, en el ejercicio de press de banca, siempre que se lleva a cabo un test progresivo bien ejecutado hasta llegar a la RM y comprobamos la relación entre los porcentajes que representan las distintas masas desplazadas y las velocidades a las que se han desplazado, encontramos un ajuste muy elevado a una curva de tendencia polinómica de segundo grado.

Este tipo de ajuste tan elevado se ha producido en la totalidad de los tests bien realizados que se han llevado a cabo por los autores en los últimos 25 años. Hay que tener en cuenta que la fase concéntrica en el test de press de banca debe realizarse después de una breve pausa (1-1,5 s) posterior a la fase excéntrica, con el apoyo de la barra en el pecho o en un soporte.

La fase concéntrica debe realizarse sin contramovimiento y la velocidad de ejecución debe ser la máxima posible ante cada masa. Se debe partir desde intensidades relativas bajas, equivalentes al 15- 20% de la RM. Un alto valor de las R2 permite estimar (aplicando las ecuaciones de regresión correspondientes) la velocidad con cualquier porcentaje de la RM con un error muy reducido.

La relación entre los distintos porcentajes y sus velocidades medias propulsivas correspondientes en el ejercicio de press de banca se expresa en la figura 1. La serie de puntos que se asemejan a una línea— que aparecen a la altura del 100% de la RM, redondeados por un circulo rojo, son los valores de la velocidad de la RM de cada uno de los sujetos. Naturalmente, hay sujetos cuya velocidad media con la RM está por encima de la media y otros por debajo. no es posible que todos los sujetos realicen su repetición máxima a la misma velocidad.

 

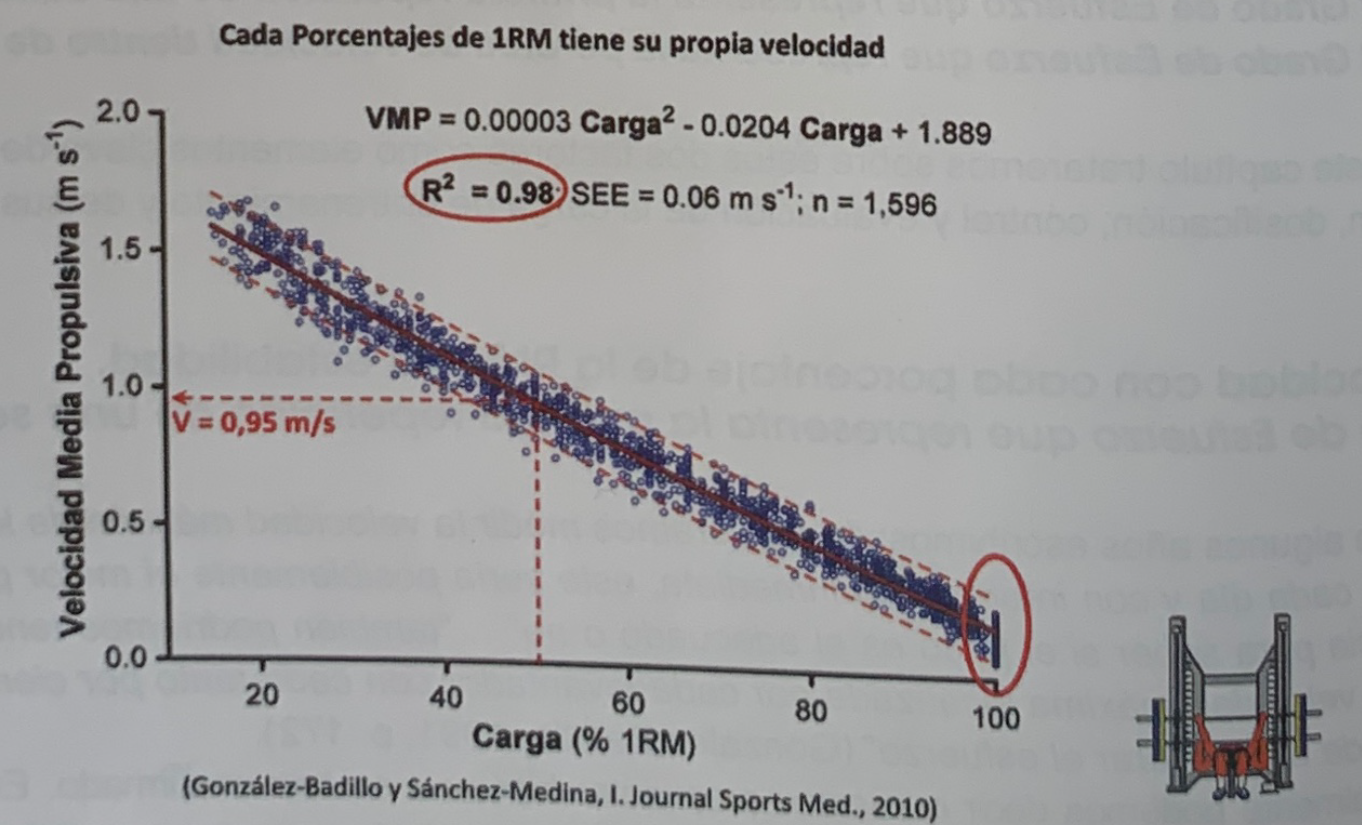
Figura 1. Relación entre los porcentajes de la RM y sus velocidades medias propulsivas correspondientes. Los 1596 datos de 176 sujetos quedan prácticamente dentro del intervalo de De 95%, con una R2 de 0,98 y un error de estimación de 0,06 (González-Badillo y Sánchez-Medina)

Estas diferencias en la velocidad de las RMs son las responsables de que los puntos vayan ligeramente por encima de la línea media o por debajo. Es decir, la velocidad de cada porcentaje tiende a depender de la velocidad con la que se alcanzó la RM.  Si con los datos de la figura 1 se considera la velocidad media propulsiva (VMP) como variable independiente, obtenemos una R2= 0,981; un error de estimación de 3,56% y la siguiente ecuación de regresión %1RM = 8.4326 * VMP2 – 73,501 * VMP + 112,33, donde VMP es la velocidad media propulsiva.

Si tomáramos tomáramos como referencia la velocidad VM, no la VMP, los datos serían los siguientes: R2 = 0,979; un error de estimación 3.77% y la ecuación: %1RM = 7,5786 VM2— 75,885 VM + 113,02, donde VM es la velocidad media de todo el recorrido.

Estas ecuaciones permiten estimar con bastante precisión el porcentaje que representa cualquier carga absoluta una vez conocida la VMP o la VM a la que se ha desplazado, siempre que la velocidad de desplazamiento haya sido la máxima posible para el sujeto

Es preferible tomar tomar como referencia la velocidad media propulsiva, ya que representa mejor el verdadero rendimiento de cada sujeto, al eliminar de la medida la fase de frenado que se produce cuando las cargas son medias o ligeras. Pero si el medidor de velocidad utilizado no registra este valor de velocidad, se puede utilizar la velocidad media, pero teniendo en cuenta que las velocidades con cada porcentaje serán ligeramente menores ante cargas ligeras y medias si se mide la VM que si se mide MP.

Si se puede medir la velocidad media o media propulsiva máxima con la que esplaza una masa, al aplicar estas ecuaciones podemos obtener el porcentaje de la RM que resenta dicha masa.

Una vez que se conoce el porcentaje que representa una determinada masa puede estimar la RM en cada momento sin necesidad de medirla, aunque el conocimiento de la RM no es necesario ni para dosificar el entrenamiento ni para valorar su efecto. Lamentablemente, son muchos los “estudios” que se han destinado a la estimación de la RM en algunos ejercicios, cuando realmente el valor de la RM, al hablar de la carga de entrenamiento, pierde práctica y totalmente su “mala” aplicación si manejamos adecuadamente la información que nos ofrece el conocimiento de la velocidad de ejecución.

Según la ecuación de regresión mostrada en la figura 1, la velocidad media propulsiva que correspondería a cada porcentaje de la RM se presenta en la figura 2.

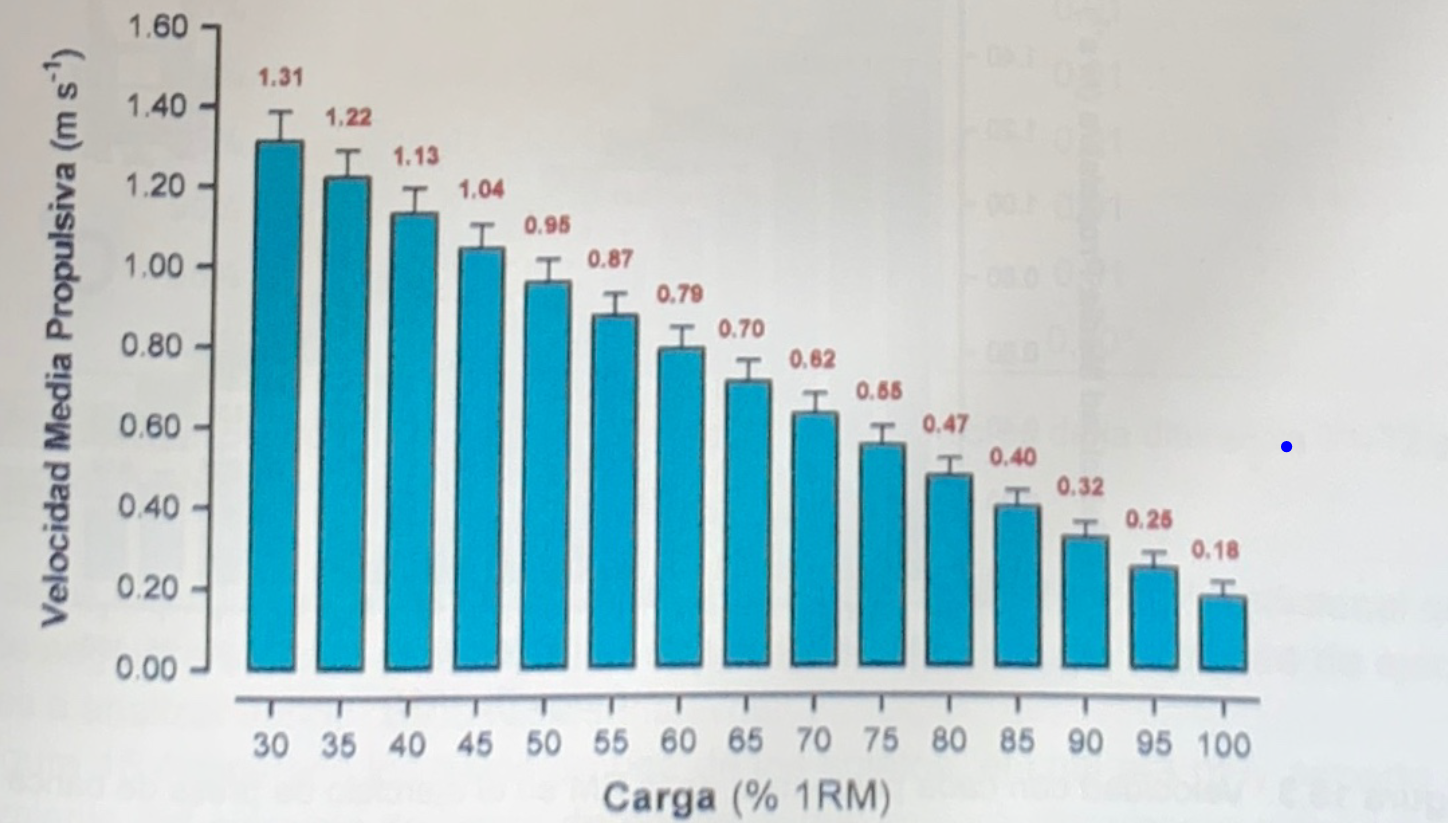
Figura 2. Velocidad media propulsiva correspondiente a cada porcentaje de la RM en el ejercicio de press de banca (González-Badillo y Sánchez-Medina, 2010)

Es muy importante comprobar que la relación entre la velocidad y la carga sea estable, es decir, sí estos valores permanecen muy semejantes cuando los sujetos cambian sus rendimientos, ya que esto es la base de la aplicación de la velocidad de la primera repetición de la serie como referencia.

La velocidad de la primera repetición de la serie sirve para determinar con qué carga relativa se está entrenando el sujeto, asi como para determinar cuál ha sido, y va siendo, el efecto del entrenamiento cada día, cuál ha sido la evolución de la intensidad máxima utilizada cada día, y cuál ha sido el efecto pre-post entrenamiento…

El efecto del entrenamiento se valora por los cambios de velocidad ante las mismas cargas absolutas en cualquier momento, que puede ser antes y después de un periodo de entrenamiento o en cada uno de los entrenamientos. Todo esto constituye parte de la máxima y mejor información de la que puede disponer un entrenador para saber lo que está haciendo y mejorar su metodología de entrenamiento.

La velocidad de la primera repetición de la serie sirve para determinar con qué carga relativa se está entrenando el sujeto

En este sentido, se aportan una serie de datos que sirven de referencia para confirmar que, efectivamente, los valores de velocidad con cada porcentaje son muy estables, aunque cambie el rendimiento de los sujetos y aunque los sujetos sean de un nivel de rendimiento muy diferente. Un primer ejemplo de esta estabilidad se presenta en la figura 3, en la que se comparan los resultados de dos mediciones de las velocidades con cada porcentaje de la RM en el ejercicio de press de banca.

primer estudio: análisis de la velocidad en el ejercicio de press de banca

Los valores al año 2010 son los mismos que los de la figura 2. Estos valores, que se registraron en los años 2006-2007, se obtuvieron con sujetos distintos a los participantes en el estudio de 2014, cuyos datos fueron registrado en 2013-14, con 6-7 años de diferencia. Se puede observar que los valores de velocidad con cada porcentaje son practicamente los mismos. Estos datos contribuyen a confirmar que la velocidad con cada porcentaje permanece estable, aunque los datos se obtengan con muestras totalmente distintas.

 

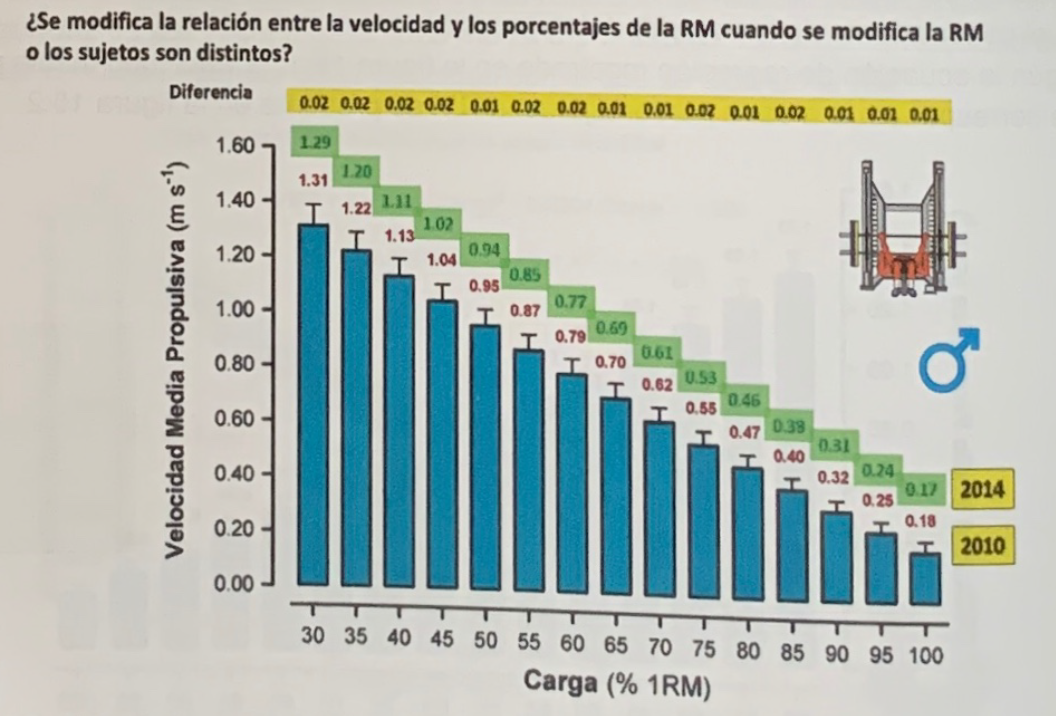
Figura 3. Velocidad con cada porcentaje de la RM en el ejercicio de press de banca en dos grupos distintos de sujetos y varios años de diferencia en el registro de los datos. Se puede observar que las diferencias (parte superior de la figura) en las velocidades no superan los 0,02 m-s-1. (Figura de Sánchez-Medina).

Siguiendo con los ejemplos, en el estudio de González-Badillo y Sánchez-Medina (2010), realizado con el press de banca, se comprobó que después de un periodo de entrenamiento de una de media de seis semanas, 56 sujetos, que mejoraron como media un 9,3% su RM en el press de banca, mantuvieron prácticamente la misma velocidad con cada porcentaje. Estos datos permiten confirmar que no solo cada porcentaje de la RM tiene su propia velocidad, sino que esta velocidad es muy estable cuando se modifica el rendimiento.

no solo cada porcentaje de la RM tiene su propia velocidad, sino que esta velocidad es muy estable cuando se modifica el rendimiento.

En la tabla 1 se expresan los valores medios de velocidad con cada porcentaje antes y después del entrenamiento de los 56 sujetos. La diferencia máxima es de 0,01 m*s-1. Hay que resaltar que estos sujetos entrenaron según su criterio, sin instrucción alguna, lo cual significa que los entrenamientos debieron ser de características muy diferentes.

 

 

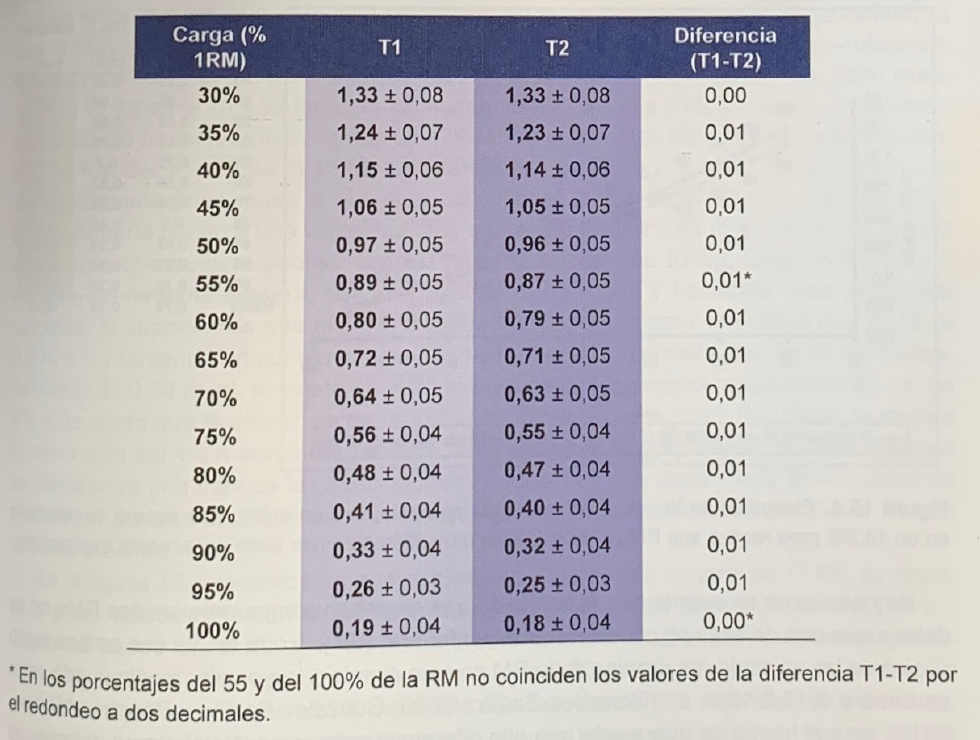
Tabla 1. Velocidad media propulsiva y desviación típica con cada porcentaje de la RM en press de banca en 56 sujetos antes (T1) y después (T2) de un periodo de entrenamiento de 9 semanas de medía (González-Badillo y Sánchez-Medina, 2010).

De los datos individuales de estos 56 sujetos podemos sacar información adicional que nos permite seguir reforzando la estabilidad de la relación porcentaje-velocidad de ejecución. Se analizan a continuación varios casos representativos.

En la figura 4 se representan los datos de uno de los sujetos, el cual era muy experto en entrenamiento del ejercicio de press de banca, y que mejoró claramente su 1RM: 14,8%. Si observamos la figura el test 2, T2 (línea roja), aparentemente , las velocidades con cada porcentaje son inferiores a las del test 1, T1 (línea azul). Esto iría en contra de la hipótesis que se mantiente, pero estos datos no son comparables, por lo que, realmente, no van en contra de la hipótesis.

La explicación está en la velocidad con la que se ha conseguido cada RM. En el T1 la velocidad fue de 0,17 m*s-1, mientras que en el T2 fue de 0,06 m*s-1(ambos valores en los círculos rojos de la parte inferior de la figura). Estas dos RMs no se pueden comparar, porque se han conseguido a velocidades claramente distintas, y, por tanto, tampoco se pueden comparar sus velocidades con cada porcentaje: cuanto menor sea la velocidad con la que se alcance la RM, menor será la velocidad con cada porcentaje.

Si la diferencia entre las velocidades de las RMs es igual a 0,03 m*s-1, ya se puede empezar a observar una tendencia a ser inferiores las velocidades correspondientes a la RM alcanzada a menor velocidad, y si las diferencias son superiores a 0,03 m*s-1, ya no deberían compararse ambas RMs.

 

 

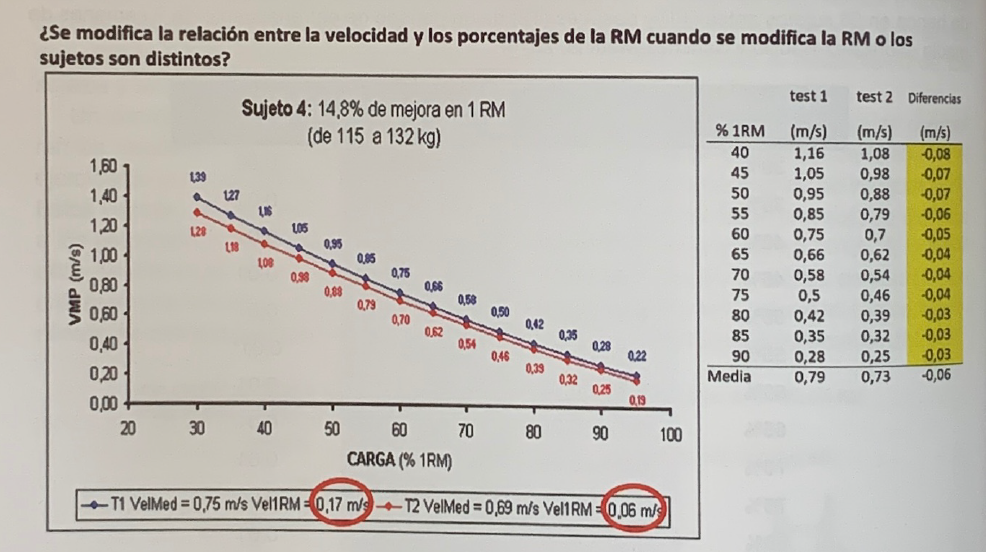
Figura 4. Evolución de la velocidad con cada porcentaje en un sujeto que supera su resultado en un 14,8% pero realiza sus RMs a velocidades muy diferentes (ver texto para mayor explicación).

Hay que tener en cuenta que el hecho de que no deban compararse las dos RMs no se debe a que una de ellas se considere una “verdadera” RM y la otra no, ya que ambas están dentro de las velocidades propias de la RM de este ejercicio, cuyo valor medio puede estar en torno a 0,17-0,18 m*s-1 (González-Badillo, 2000; González-Badillo y Sánchez-Mediná 2010), sino al hecho de que existe una alta diferencia entre ellas.

No obstante, a pesar de que en el T1 casi se triplica la velocidad del T2, las diferencias en las velocidades con cada porcentaje no llegan a superar, en el peor de los casos (porcentajes bajos), el 5% de la RM dado que la diferencia en velocidad cada un 5% es de 0,08-0,09 m*s-1, diferencia que no se supera en ninguno de los porcentajes calculados, desde el 30 (0,09 m*s-1 de diferencia) hasta el 95%.

COnclusiones del primer estudio

Como resultado del análisis de este caso, se pueden deducir, al menos, las siguientes aplicaciones prácticas:

1) no se pueden comparar RMs cuyas velocidades de medición sean superiores a 0.03 m*s-1, aunque en casos extremos como el que estamos sentando, en el que se triplica la velocidad de la RM, los efectos no vayan más allá de una diferencia del 5% de la RM para la misma velocidad del mismo sujeto,

no se pueden comparar RMs cuyas velocidades de medición sean superiores a 0.03 m*s-1,

2) dada la alta probabilidad de que dos RM se midan a velocidades distintas, no es recomendable medir nunca la RM (se puede estimar, si fuera necesaria para algo, como veremos en otro apartado) y

3) solo midiendo la velocidad con la que se alcanza la RM, se puede tener la información necesaria para evitar los errores cometidos con alta frecuencia al medir esta variable.

Aquí hemos de recordar que la verdadera RM nunca se va a conocer, pero se pueden considerar algunas RMs como “verdaderas” o representativas de la RM verdadera cuando se midan a velocidades propias de sus correspondientes valores de RM. Cuanto más se aleje la velocidad medida (siempre velocidades superiores) de los valores propios de la RM de un ejercicio, más “falsa” es la medición de la RM. Esto, una vez más, solo se puede saber si se mide la velocidad con la que se realiza el ejercicio.

Los errores a los que hacemos referencia en la aplicación práctica 3) se refieren a que la mayoría de los cambios como son la mejora o empeoramiento de los resultados observados cuando se mide 1RM son falsos, pues si un sujeto, por ejemplo (es un caso real), levanta 82 kg en el T1y 92 kg en el T2, se puede concluir tras hacer los cálculos, que el sujeto ha mejorado su marca un 12%.

Pero si se tiene en cuetna que este sujeto hizo la RM del T1 a 0,33 m*s-1 (datos reales) y la del T2 a 0,2 m*s-1, la conclusión es falsa, pues si el sujeto pudo hacer la RM en el T2 a 0,2 m*s-1, también podría haberla hecho a una velocidad muy semejante (0,2 + 0,02 m*s-1) en el T1.

Esto significaría que hubiera podido levantar un peso mayor que 82 kg, luego la mejora no ha sido, de ninguna manera, del 12%. A título de ejemplo, y haciendo unos pequeños cálculos, si suponemos que el T1 lo hubiera hecho a la misma velocidad que el T2, a 0.2 m*s-1, y teniendo en cuenta que cada un 5% el cambio de velocidad es de aproximadamente de 0,08 m*s-1, el sujeto en el T1 hubiera levantado aproximadamente 88 kg, un 8% más, dado que la diferencia entre el T1 y el T2 es de 0,13 m*s-1.

Por tanto, la mejora hubiera sido del 4-5% aproximadamente, muy lejos del 12% aparente. De este ejemplo se desprende una más de las aplicaciones importantes que tiene medir la velocidad de me ejecución, aunque esta aplicación es mejor que no haya que usarla, porque la RM no pez debería medirse nunca.

Segundo estudio

En la figura 5 se muestra un nuevo ejemplo. Este sujeto mejoró un 11.8% su resultado y las velocidades con la RM presentaron una pequeña diferencia de 0,02 m*s-1. Como se puede observar, las velocidades con cada porcentaje permanecieron prácticamente estables, con una diferencia máxima de 0,02 m*s-1, es decir, el equivalente a una diferencia máxima del 1,25% de la RM con respecto al T1.

Además, en este caso, la velocidad en todos los porcentajes tendió a subir ligeramente, con lo que se podría ss decir que el sujeto mejoró ligeramente (porque el cambio solo puede ser muy pequeño) su déficit de fuerza. Esta ligera mejora de la velocidad puede venir explicada porque el sujeto, después de su experiencia al hacer los tests, decidió entrenar realizando cada el repetición a la máxima velocidad posible, cuando anteriormente lo hacía lentamente de manera voluntaria.

Por tanto, se confirma que a pesar de una mejora considerable de casi el 12% (en este caso podemos decir que real), las velocidades con cada porcentaje permanecen estables.

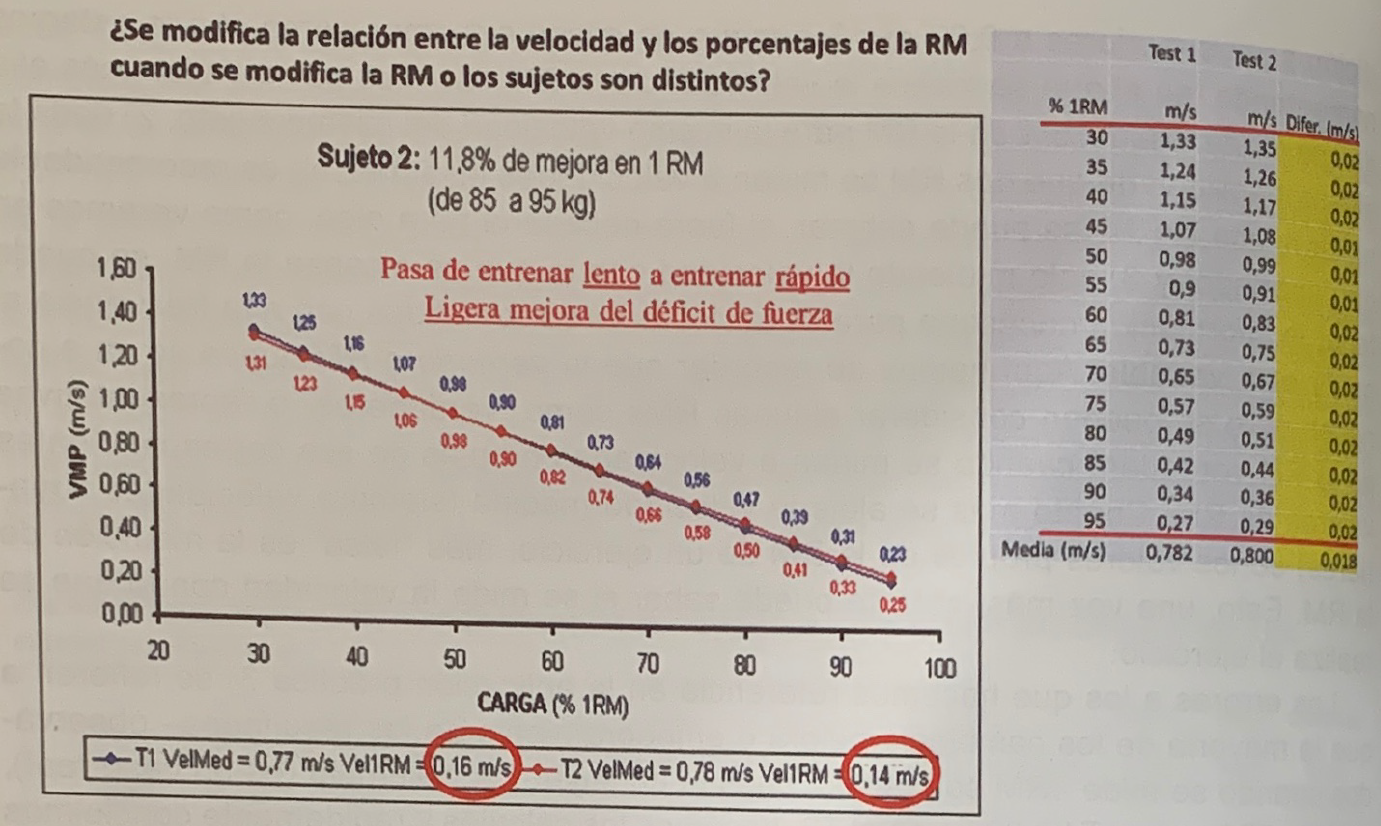
Figura 5. Evolución de la velocidad con cada porcentaje en un sujeto que supera su resultado en un 11,8% y realiza sus RMs a velocidades muy semejantes

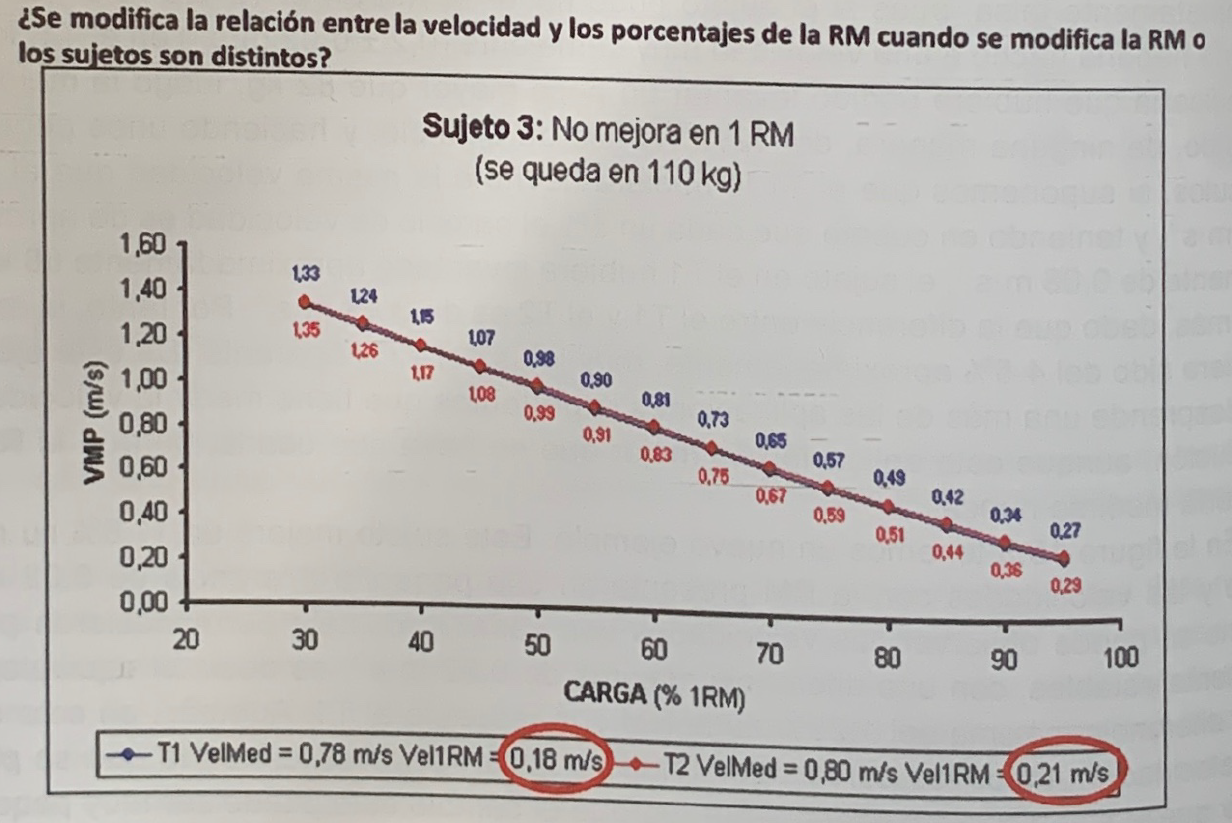
Figura 6. Evolución de la velocidad con cada porcentaje en un sujeto que no supera su resultado y realiza sus RMs a velocidades muy semejantes

En la figura 6 se muestra un ejemplo de un sujeto que no mejoró su resultado y que las velocidades con cada porcentaje fueron prácticamente iguales en ambos tests, aunque el T2 se realizó a una velocidad de 0,03 m*s-1 superior que la del T1.

Pero, precisamente, esta pequeña diferencia de velocidad podría explicar, por una parte, por qué las velocidades en el T2 son mínimamente superiores (0.01-0.2 m*s-1), y por otra, que realmente no se puede decir que el sujeto no mejoro nada su rendimiento, ya que mejoró la velocidad 0,03 m*s-1 ante la misma carga (110 kg). Esta valoración solo se puede hacer si se mide la velocidad de ejecución

En la figura 7 se puede observar el caso de un sujeto que mejoró su RM un 7,9%, que realizó sus dos RMs a la misma velocidad, pero que la velocidad con cada porcentaje hasta el 75% de la RM tendió a disminuir. Este fue el único caso, de 56, que se apartó de que venimos manteniendo. Pero al consultar al sujeto sobre su forma de entrenar, manifesto que entrenó lentamente de manera voluntaria.

Entrenar lentamente de forma voluntaria puede tender a disminuir proporcionalmente el rendimiento con cargas que se desplazan a alta velocidad y aumentar así el déficit de fuerza ante estas cargas

Esta forma de entrenar puede tender a disminuir proporcionalmente el rendimiento con cargas que se desplazan a alta velocidad y aumentar así el déficit de fuerza ante estas cargas. A pesar de esta circunstancia, se puede observar que la disminución de la velocidad con cargas ligeras no sobrepasó los 0,06 m*s-1, lo cual significa que, en el peor de los casos, la diferencia máxima en velocidad con cada porcentaje en el T2 con respecto al T1 fue equivalente al 3,7% de la RM.

Figura 7, Evolución de la velocidad con cada porcentaje en un sujeto que supera su resultado en un 7,9% y realiza sus RMs a la misma velocidad.

En la tabla 2, compuesta por dos grupos de datos, con un total de 20 sujetos (los 20 primeros, por un orden aleatorio, en la lista de los 56 sujetos que repitieron los tests) podemos observar la velocidad a la que alcanzaron sus RMs en los tests 1 y 2, la velocidad media de los porcentajes desde el 40 al 90% de la RM, la máxima y la mínima diferencia obtenida en el cojunto de estos porcentajes y el cambio en el rendimiento.

Se observa que la velocidad media desde el 40 al 90% sigue la misma tendencia que la diferencia entre las velocidades de las RMs. Solamente en los casos de los sujetos JG y PC la diferencia máxima en algún porcentaje es equivalente al 5% de diferencia con respecto a la RM.

Puede observarse que hay 12 casos de mejoras que van desde el 8.3 al 21.23% con una media del 13.9%, en los que la diferencia máxima en la velocidad con los porcentajes desde el 40 al 90% es de 0.05 m*s-1 en los dos sujetos mencionados anteriormente (JG y PC), un caso con 0.04 m*s-1 (V) y el resto con 0.03 m*s-1 o menos. Este conjunto de datos viene de nuevo a reforzar la estabilidad de la velocidad de cada porcentaje, aunque se produzcan cambios importantes en el rendimiento de la RM.

 

 

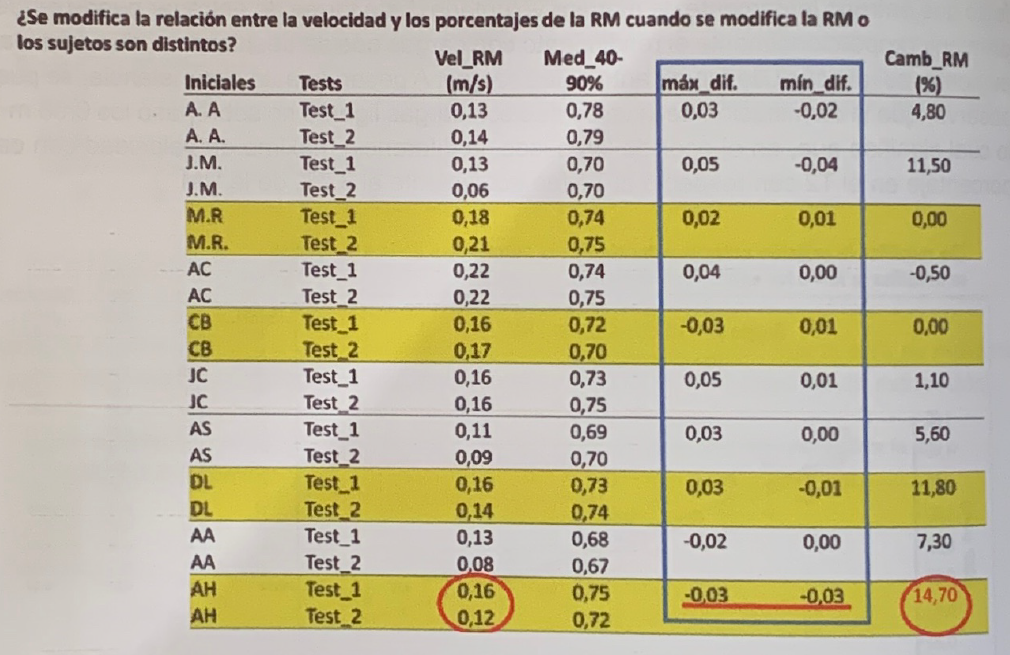
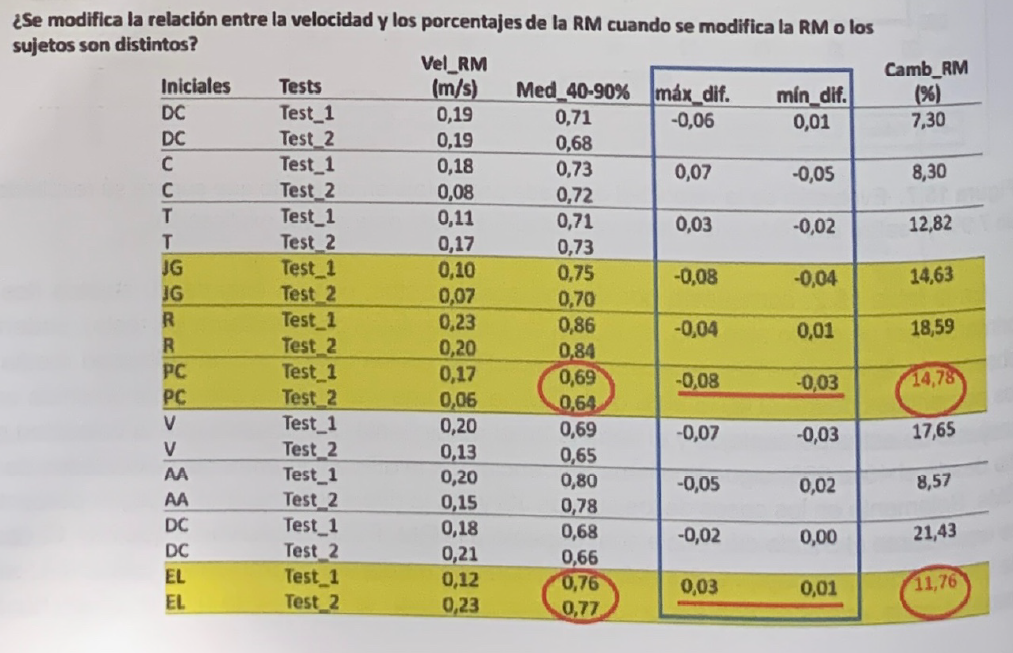
Tabla 2 Valores de velocidad con la RM (vel_RM), velocidad media de las velocidades con los porcentajes comprendidos entre el 40 y el 90%, máxima (max_dif), y mínima(min_dif) diferencia de velocidad con cada porcentaje entre los test 1 y 2 y cambio en el rendimiento (Camb_RM) de los 20 primeros sujetos en la lista de 56 que repitieron los tests. 

En la tabla 3 se pueden observar las velocidades con las RMs, velocidades medias desde el 40 al 90% de las RMs, diferencias en la velocidad con la RM y las diferencias entre las velocidades de medias con el conjunto de los porcentajes en dos tests para los mismos sujetos incluidos en la tabla 2. Tomando el conjunto de los datos incluidos en las columnas amarillas, se puede calcular la relación entre las diferencias en la velocidad de la RM y las diferencias en la velocidad media de

 

 

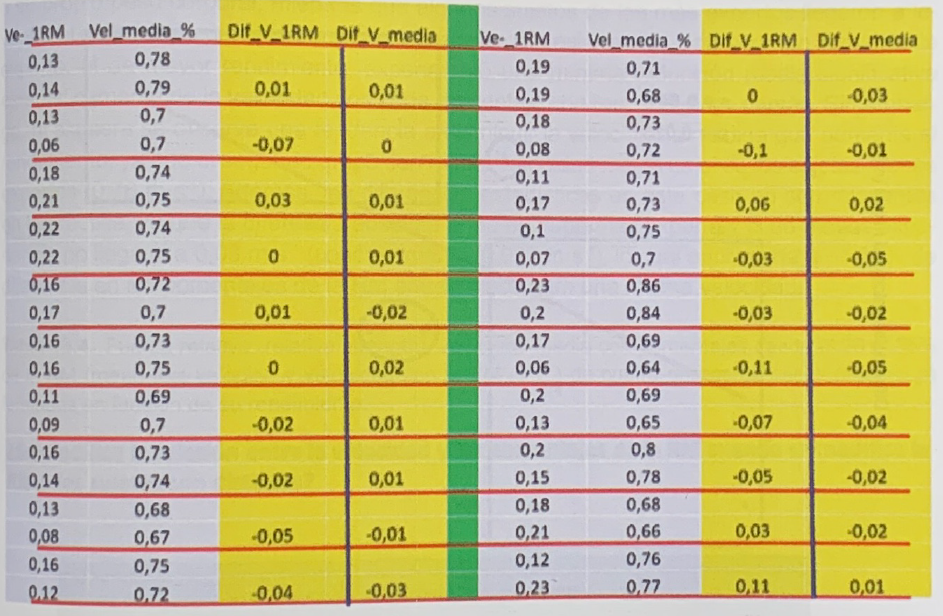
Tabla 3. Velocidades con las RMs (Ve_1RM), velocidades medias de los porcentajes desde el 40 al 90% de las RMs (Vel_media_%), diferencias en la velocidad con la RM (Dif_V_1RM) y las diferencias entre las velocidades medias con el conjunto de los porcentajes en los dos tests (Dif_V_media) de los mismos sujetos incluidos en la tabla 2.

En la figura 8 se presenta la relación entre las diferencias en la velocidad con la que se consiguieron las RMs (eje X) y las diferencias en la velocidad media en los porcentajes de la RM desde el 40 al 90% (eje Y).

Se puede observar que 12 de los 20 casos se encuentran en los cuadrantes positivos de los ejes de coordenadas, que son los que se corresponden con la tendencia que indica que a velocidad de la RM determina la velocidad con cada porcentaje, es decir, cuanto mayor es la velocidad de la RM mayor tiende a ser la velocidad con cada porcentaje.

Hay tres casos en los que las velocidades con la RM fueron iguales (puntos que coinciden con el eje Y) y las velocidades con los porcentajes cambiaron minimamente, entre 0,03 y 0,02 m*s-1.

Un caso en el que habiéndose producido una disminucion de la velocidad de la RM en T2 en unos 0,07 m*s-1, la velocidad media de los porcentajes fue idéntica (punto que se encuentra en el eje X). Este caso puede considerarse como un ejemplo de un sujeto que mejoró su déficit de fuerza: aunque a una velocidad menor de la RM le debería corresponder una velocidad ligeramente inferior con cada porcentaje, el sujeto mantuvo una velocidad.

Hay dos casos en el cuadrante negativo inferior en el que habiendo aumentado ligeramente la velocidad con la RM alrededor de 0,02 m*s-1, la velocidad con los porcentajes disminuyó 0,02 m*s-1, lo que sugiere que se produjo un mínimo aumento del deficit de fuerza.

Por último, hay un caso en el cuadrante negativo superior en el que un sujeto que realizó su velocidad de la RM a menor velocidad (0,02 m*s-1) en el T2, aumentó ligeramente la velocidad con los porcentajes (0,01 m*s-1).

Como se puede deducir, la estabilidad de la velocidad con cada porcentaje se ratifica. Los cambios son mínimos y la tendencia entre la velocidad con la RM y la velocidad con cada porcentaje se cumple de manera notable.

 

 

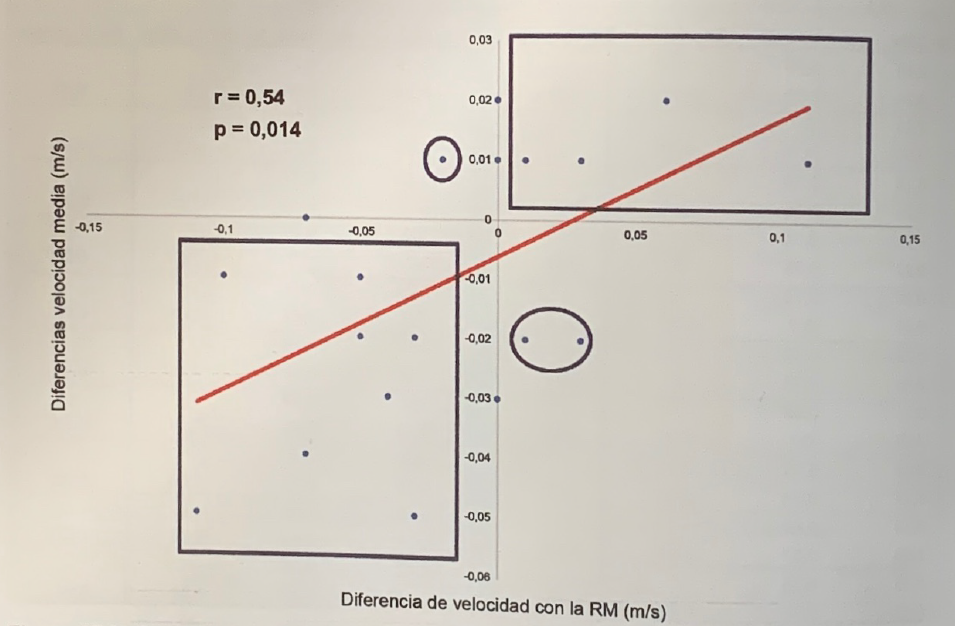
Figura 8. Relación entre las diferencias en la velocidad con la que se consiguieron las RMs (eje X) y las diferencias en la velocidad media en los porcentajes de la RM desde el 40 al 90% (eje Y).

Debe tenerse en cuenta que los sujetos no pueden comportarse como “máquinas” perfectas, sino que responden de manera no exactamente igual ante una serie de cargas progresivas cuando se pretende realizar un test de 1RM. Esto quiere decir que ante una carga absoluta el rendimiento no es exactamente el mismo que ante la carga absoluta inmediatamente superior.

Es decir, si un sujeto consigue una velocidad determinada a una carga absoluta, no siempre en la carga inmediatamente superior, que representará un aumento porcentual determinado, va a responder alcanzando exactamente la velocidad que correspondería a ese aumento porcentual de la carga. Esto puede hacer que la curva fuerza o carga-velocidad del sujeto se ajuste en mayor o menor medida a su verdadera capacidad de rendimiento, dando lugar a pequeñas desviaciones del modelo que representa a la población a la que pertenece el sujeto.

¿Afecta el nivel rendimiento a la velocidad?

Para seguir añadiendo elementos de confirmación de la estabilidad de la velocidad con cada porcentaje, se podría valorar si la velocidad con cada porcentaje es semejante o no entre personas con distinto nivel de rendimiento.

De los resultados del estudio se deduce que, efectivamente, la velocidad con cada porcentaje es muy semejante entre personas con un nivel de rendimiento muy distinto. Al dividir el grupo de 176 casos en cuatro grupos en función de su RM relativa (RM * peso corporal-1), las velocidades medias desde el 30 al 95% de la RM fueron de 0.76, 0.77, 0.77 y 0.73 m*s-1 (tabla 4), en este orden, desde el grupo de menor rendimiento al grupo mas experto, respectivamente.

Por tanto, la velocidad media es prácticamente la misma a pesar de que el rendimiento aumente de manera considerable. Piénsese que los sujetos con menor rendimiento no llegaban a levantar en press de banca un peso equivalente a su propio peso corporal, mientras que algunos sujetos de los más expertos llegaron a levantar el doble de su peso corporal o se aproximaron a esta marca.

sujetos con menor rendimiento no llegaban a levantar en press de banca un peso equivalente a su propio peso corporal, mientras que algunos sujetos de los más expertos llegaron a levantar el doble de su peso corporal

Solo el grupo sumamente experto, el de mayor rendimiento, experimentó una mínima reducción media significativa estadísticamente de la velocidad con cada porcentaje con respecto a los demás. Sin embargo, ni siquiera se observa una tendencia a disminuir la velocidad a medida que aumenta el rendimiento, ya que el segundo grupo con menor velocidad media es el de los sujetos menos expertos (0,76 m*s-1).

Además, las diferencias estadísticas en este caso no son relevantes en la práctica, ya que la diferencia absoluta entre el grupo más experto y el de menos experencia no llega ni a 0,03 m*s-1 (concretamente, 0,027 m*s-1), lo cual equivaldría a -1,69% de diferencia en los porcentajes de la RM entre ambos para una misma velocidad.

 

 

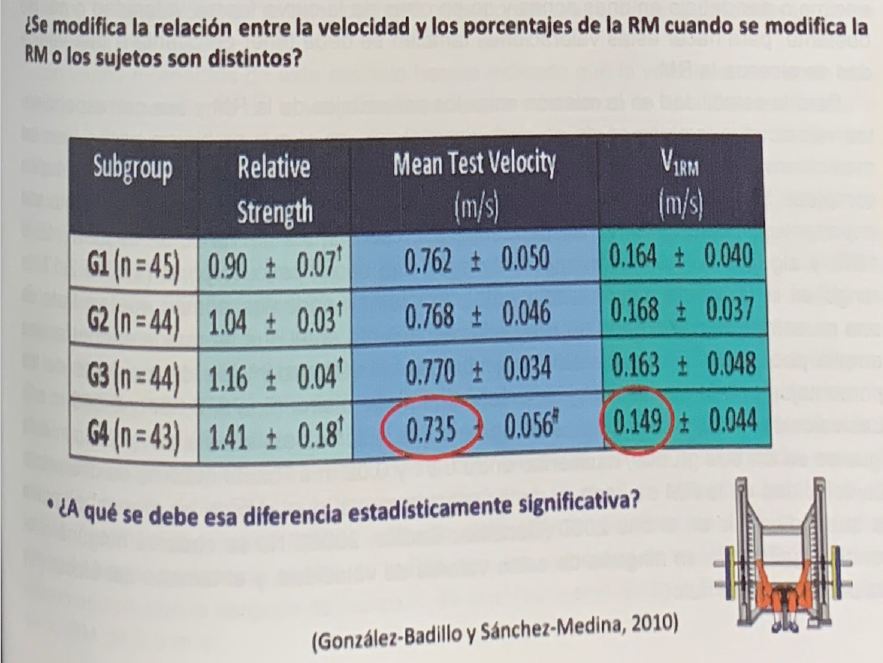
Tabla 4. Fuerza relativa (relative strength), velocidad media con porcentajes desde el 30 al 95% de la RM (mean test velocity) y velocidad con la RM (V1RM) de cuatro grupos de casos (subgroup) formados en función de su rendimiento.

No obstante, si se analizan con mayor profundidad estos resultados, se lelga a la conclusión de que estas diferencias no son reales. Respondiendo a la pregunta formulada en la parte inferior de la tabla 4, la aparente menor velocidad con cada porcentaje del grupo más experto se debe a que la velocidad media con la que alcanzan los componentes de este grupo su RM es ligeramente menor que la de los demás (0,045 m*s-1 con respecto al grupo de menor rendimiento, y 0,019 y 0,014 m*s-1 para los otros dos grupos).

Este hecho ocasiona que, necesariamente, la velocidad con cada porcentaje tienda a ser menor, lo que viene a ratificar, de nuevo, lo que ya se ha puesto de manifiesto anterioremente. Por tanto, la ligera reducción de la velocidad con cada porcentaje del grupo de más rendimiento en el ejercicio de press de banca se debe a la tendencia a disminuir la velocidad con la RM en sujetos extremadamente expertos.

Es razonable aceptar que estos sujetos son capaces de aprovechar en mayor medida su propio potencial de fuerza, debido a que tienen más confianza en sus posibilidades y mejor técnica al ejecutar el ejercicio. Es conveniente destacar que, dadas las características de los sujetos de este estudio, la generalización de estos datos nos lleva a poder aplicarlos a toda la población, dado que en el grupo se encuentran sujetos que levantan desde menos del 90% de su peso corporal hasta sujetos que levantan el doble de su peso corporal.

Esto significa que aquí puede estar incluida cualquier persona joven practicante de cualquier deporte o simplemente como usuario del entrenamiento de fuerza. Por tanto, este es uno de los pocos ejercicios que realmente permitiría valorar nuestro “perfil” de fuerza-velocidad.

Si ejecutamos bien el ejercicio, podremos saber en qué medida nuestro rendimiento en este ejercicio está en la media de la población en cuanto a la velocidad con cada porcentaje, si está ligeramente por encima o si está ligeramente por debajo, o incluso, si está por encima o por debajo en unas zonas y no en otras de la curva fuerza-velocidad o no.

No obstante, para hacer estas valoraciones también se debe tener en cuenta a qué velocidad se alcanza la RM. Pero la estabilidad en la relación entre los porcentajes de la RM y sus correspondientes velocidades también se da en cualquier ejercicio en el que se hayan hecho bien las mediciones.

En la tabla 5 aparecen los datos correspondientes al ejercicio de sentadilla completa. El grupo estuvo formado por 80 sujetos. Las diferencias en el rendimiento son importantes, desde 93 a 126 kg de media, con coeficientes de variación desde el 12 al 18%, y algunos sujetos levantando más del doble de su peso corporal (1,57 a 2,17 de rango en el grupo de mayor rendimiento).

Por lo que podemos admitir que se trata de una muestra que comprende un rango de rendimiento en el que se puede encontrar una amplia población de deportistas.

la velocidad media del conjunto de los porcentajes es prácticamente la misma

Sin embargo, la velocidad media del conjunto de los porcentajes (mean test velocity) es prácticamente la misma (0,873, 0,867 y 0,865 m*s-1) Las velocidades con los ejemplos de porcentajes incluidos en la tabla son prácticamente iguales en los tres grupos, existiendo entre 0,01 y 0,02 m*s-1 como máximo de diferencia. La velocidad de la RM de cada grupo es prácticamente igual a la de los demás, e igual a la que indicamos en el año 2000 (González-Badillo, 2000). No se observa ninguna pe rencia significativa en ninguno de estos valores de velocidad

 

 

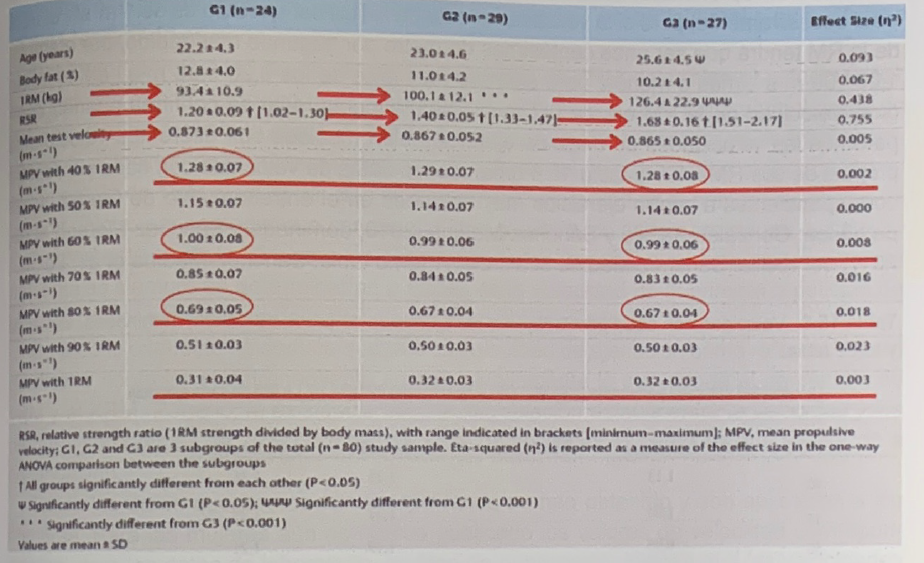
Tabla 5. Comparación de las velocidades medias de los tests con porcentajes desde el 30 al 95% de la RM (mean test velocity), velocidad media propulsiva con distintos porcentajes (MPV), velocidad media propulsiva con la RM (MPV with 1RM) en tres grupos formados en función de su rendimiento vativo con respecto al peso corporal (RSR) en el test de sentadilla completa. El tamaño del efecto viene representado por el estadístico “eta” (effect size n2) (Sánchez-Medina et al., 2017).

Por tanto, en un ejercicio tan diferente del press de banca como es la sentadilla, se confirma la estabilidad de la velocidad con cada porcentaje, aunque el rendimiento de los sujetos sea muy distinto. Se ha indicado que la velocidad con cada porcentaje es dependiente de la velocidad con la que se alcanza la RM. Esta tendencia se ha podido constatar al analizar los distintos ejemplos de rendimiento con el ejercicio de press de banca.

Aunque esta tendencia no solo se da en un mismo ejercicio cuando cambia la velocidad de la RM por su medición defectuosa, sino que, naturalmente, también se da entre los distintos ejercicios, porque cada ejercicio tiene su velocidad propia, y distinta la de los demás, de su RM (González-Badillo, 2000).

En este artículo, publicado con datos registrados en los años 90, ya se comentaba que la velocidad con el 40% de la RM del press de banca era de 1,15 m*s-1, lo que se diferencia en solo dos centésimas de m*s-1 de los datos actuales (1,13 m*s-1), y la sentadilla presentaba una velocidad de 0,93 m*s-1′ con el 64,3% de la RM, prácticamente, la misma velocidad que se propone actualmente (0,92 m*s-1 con el 95%. ver tabla 6).

cada ejercicio tiene su velocidad propia, y distinta la de los demás

Así mismo, se confirmaba ya que la velocidad con cada porcentaje dependía de la velocidad propia de la RM, porque la arrancada, con una velocidad media de la RM de 1,04, la velocidad de 1,15 m*s-1 se obtenía con el 91% de la RM, mientras que, como hemos indicado, esta misma velocidad de 1,15 m*s-1 con el press de banca pertencía al 40% de la RM, con una velocidad de su RM de 0.2 m*s-1. Lo mismo ocurría con la cargada de fuerza: 1.09 m*s-1 para el 87% de la RM y una velocidad de su RM de 0.9 m*s-1.

El hecho de que la velocidad con cada porcentaje dependa de la velocidad de la RM es tan evidente, que podemos decir que es de “perogrullo”, aunque esto no impide que en alguna ocasión a alguien le dé por ponerlo en duda.

Es evidente que si la velocidad propia de la RM de un ejercicio es, por ejemplo, 0,2 m*s-1, la velocidad del 95% de la RM de ese ejercicio debe ser aproximadamente de 0,26-0,28 m*s-1, y el 90% debe ser de 0,32-0,34 m*s-1 y así sucesivamente, pero si la velocidad propia de la RM del ejercicio es de 1 m*s-1, el 95% de la RM tendrá que ser unas centésimas de metro por segundo más rápido, por ejemplo, 1,08-09 m*s-1, más o menos, pero siempre muy lejos de los 0,26-0,28 m*s-1 del ejercicio cuya velocidad de la RM era de 0,2 m*s-1.

Naturalmente, esto se confirma cuando se comparan las velocidades de distintos ejercicios bien medidos con diferentes velocidades propias de sus RMs.

En la tabla 6 aparecen los datos de velocidad con cada porcentaje correspondientes a cuatro ejercicios muy comunes en el entrenamiento de fuerza (press de banca: González-Badillo y Sánchez-Medina, 2010; dominadas: Sánchez-Moreno et al.. 2017; sentadilla: Sánchez-Medina et al., 2017; remo tabla: Sánchez-Medina et al., 2014).

 

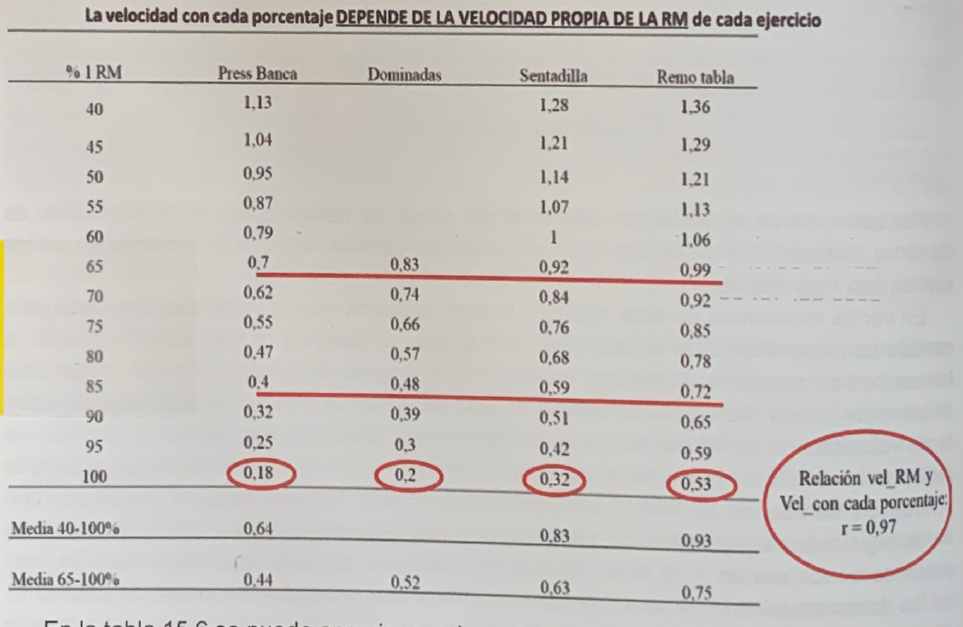
Tabla 15.6. Velocidad con cada porcentaje en los ejercicios de press de banca, dominadas, sentadilla y remo tabla.

En la tabla 6 se puede apreciar que los valores de velocidad de cada porcentaje van aumentando a medida que aumentan las velocidades propias de las RMs. La relación entre las velocidades de las RMs y la velocidad media de todos los porcentajes desde el 65% hasta el 100% es casi perfecta (r= 0,97; p < 0,05).

Es muy relevante que con solo 4 pares de datos la correlación resulte estadísticamente significativa. Por tanto, se confirma que, efectivamente, la velocidad con cada porcentaje es dependiente de la velocidad de la RM del ejercicio, así como de las diferencias en la velocidad de medida de la RM cuando esta se mide más de una vez dentro de cada ejercicio.

Como sintesis de todo lo expuesto se confirma que se puede controlar el entrenamiento a través de la velocidad de la primera repetición en la serie que siempre que se realice a la máxima velocidad posible, y esto se basa en que podemos partir del supuesto de que si bien el valor de 1RM puede cambiar entre los distintos días, la velocidad a la que se realiza cada porcentaje de la RM es muy estable.

se confirma que se puede controlar el entrenamiento a través de la velocidad de la primera repetición en la serie que siempre que se realice a la máxima velocidad posible

Por tanto el control de la velocidad nos puede informar con alta precision sobre qué porcentaje real o qué esfuerzo se está realizando en cada momento. Por tanto la velocidad propio de cada porcentaje de 1RM determina el esfuerzo real. Esto significa que la velocidad de la primera repetición de una serie determina el grado de esfuerzo que representa la carga.

Asi, la carga (masa) de entrenamiento se pordrá determinar por la velocidad de la primera repetición. Si esto es asi, lo que se debe programar no es el porcentaje de 1RM ni un XRM, sino la velocidad de ejecución de la primera repetición de la sere. Nota: por comodidad o por resultar mas intuitivo, se podría programar por medio de los porcentajes de la RM, pero las cargas absolutas(masas) que corresponden a esos de los porcentajes siempre se determinarían a través de la velocidad de la primera repetición de la serie, no por el resultado del calculo aritmetico del porcentaje.

conclusiones

De todo lo expuesto se deduce que usar la velocidad de ejecución como referencia para dosificar y controlar el entrenamiento supera ampliamente  lo que aporta el porcentje de 1Rm y XRM. Por ello, la existencia de una alta relación estable entre la velocidad y los distintos porcentajes de 1RM permite una serie de aplicaciones como las que se indican a continuación.

Todos los datos  que se han aportado se han obtenido y son aplicables a los hombres. Para las mujeres aun no se han publicado los valores de velocidad correspondientes, pero los datos de laboratorio, en fase de publicación, indican que las velocidades con cada porcentaje son prácticamente las mismas con mujeres desde una intensidad relativa del 45-50%, reduciendose aproxidamdamente en 0,03, 0,04 y 0,06 m*s-1 con las intensidades del 40, 35 y 30% de la RM, respectivamente.

las velocidades con cada porcentaje son prácticamente las mismas con mujeres

El conocimiento de la velocidad de la primera repetición (velocidad con cada porcentaje) permite:

• Evaluar la fuerza de un sujeto sin necesidad de realizar en ningún momento un test de 1RM ni un test de XRM o nRM.
• Determinar con alta precisión qué porcentaje real está utilizando el sujeto nada mas realizar, a la máxima velocidad posible, la primera repetición con una carga absoluta determinada.
• Estimar / medir la mejora o no en el rendimiento CADA DÍA sin necesidad de realizar ningún test, simplemente midiendo la velocidad con la que se desplaza una carga absoluta. Si, por ejemplo, la diferencia en velocidad entre el 70 y el 75% de la RM de un ejercicio concreto es de 0.08 m*s-1, cuando el sujeto aumente la velocidad en 0.08m*s-1, ante una misca carga absoluta, existe una probabilidad muy alta, casi del 100% de que la carga con la que entrena represente un 5% menos de intensidad. Naturalmente, si lo que se produce es una perdida de velocidad ante una misma carga absoluta (kg), podemos estar bastante seguros de que el sujeto está por debajo de su rendimiento anterior, y en una medida proporcional a la perdida de velocidad ante la misma carga absoluta.
•  La medición de la velocidad de la primera repetición de manera diaria, semana simplemente antes y después del entrenamiento permite:
  • Conocer el grado y el tiempo de adaptación de manera individual.
  • Descubrir el grado de disparidad de las respuestas de adaptación.
  • Comprobar el efecto de la mejora de la fuerza sobre otros tipos de rendimiento entrenados o no.

Con respecto a la velocidad propia de la RM se puede concluir que:

• La única vía para poder considerar una RM como “verdadera” o falsa es medir la velocidad con la que se consigue.
• Dos valores de RM del mismo sujeto no se pueden comparar sí los valores de las velocidades con las que se han medido no son iguales o muy semejantes.
• Si las velocidades a las que se han medido las RMs pre-post entrenamiento son distintas, con diferencias mayores o iguales a 0,03 m*s-1, estas RMs no son equivalentes, por lo que comparar los valores de las RMs (pesos levantados) pre-post entrenamiento llevaría a decisiones erróneas, considerando que se han producido unos cambios de fuerza (en la RM) que no son reales.
• Además, las velocidades con cada porcentaje serían aparentemente distintas, sin que signifique que realmente lo sean.

Con relación a la valoración del efecto del entrenamiento se concluye que:

• No es necesario ni se debería medir nunca la RM.
• El mejor procedimiento para la valoración del efecto del entrenamiento es volver a medir la velocidad alcanzada ante las mismas cargas absolutas que se midieron en el test inicial.
• Este procedimiento es el más coherente y preciso, ya que el efecto del entrenamiento de fuerza se mide por el cambio de velocidad ante la misma carga absoluta o como ya se ha indicado, la valoración del efecto del entrenamiento a través de los cambios en la RM, incluso en el supuesto, no muy probable, de que las velocidades con las que se midan las RMs sean iguales o muy semejantes, solo nos informaría sobre el efecto del entrenamiento ante la carga máxima (RM), pero no ante otras cargas inferiores

Otras aplicaciones:

• Utilizar el entrenamiento de fuerza con todos los sujetos, desde los niños hasta los deportistas mas avanzados o los adultos y personas mayores que pretenden mejorar su salud, sin necesidad de hacer tests de máximo esfuerzo (1RM, o XRM, por ejemplo) en ningún caso.

La propuesta de los autores, por tanto, es que siempre debería usarse la velocidad media propulsiva de la primera repetición para programar, dosificar y evaluar la carga de entrenamiento y el rendimiento del sujeto.